Tensor Commits Protocol
The security base of Theseus: public verifiability and tamper-proof computations with <1% overhead.
Overview
Tensor-commit protocols enable verifiable ML by proving a model was executed correctly. Traditional verification via recomputation is prohibitively expensive for large models.
Theseus' Tensor Commits provide batch verification and reduce opening costs through a novel application of KZG commitment schemes extended to multi-dimensional tensor structures.
How Tensor Commits Work
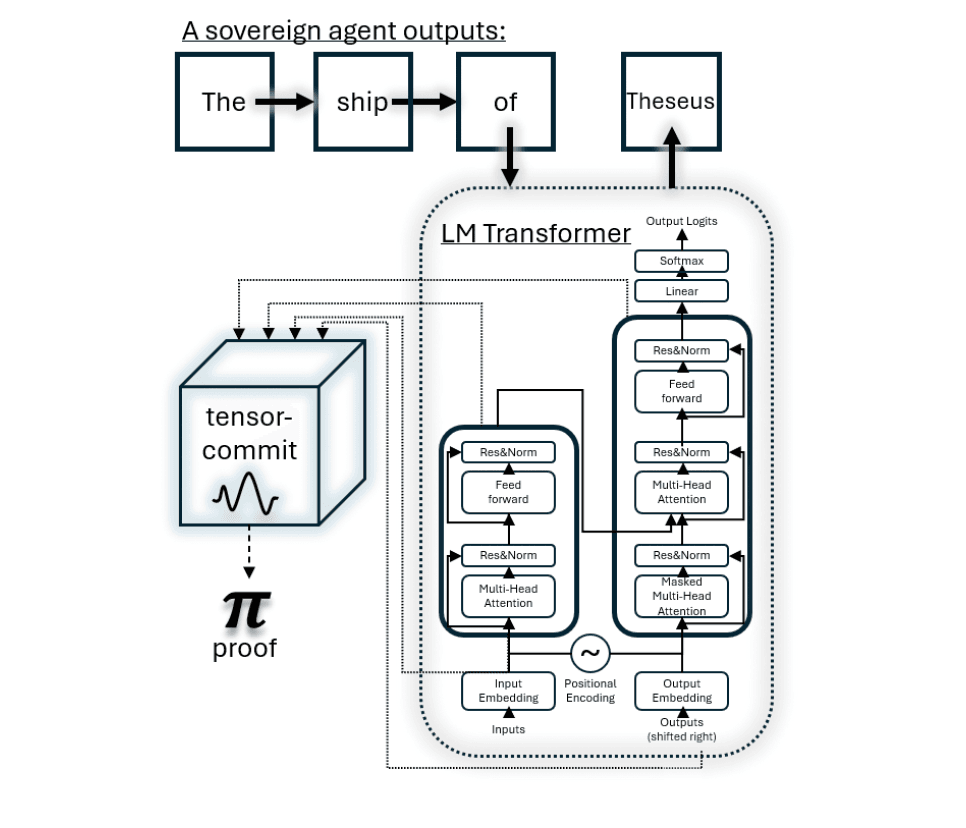
Figure Explanation
Key Achievements
<1% Proof Generation
Minimal impact on inference performance. Practical for production workloads.
<0.1% Verification Time
Verifiers check proofs in milliseconds. Thousands can audit simultaneously.
Efficient & Scalable
Terkle Trees
A Terkle tree (tensor Merkle tree) has leaves that are sub-tensors and internal nodes that carry tensor commitments instead of hash values.
Structure
- • Each dimension j has mⱼ blocks
- • Each leaf cℓ is a commitment of sub-tensor Tℓ
- • Parents commit to children tensor concatenation
- • Root cᵣₒₒₜ is the global model fingerprint
Benefits
- • Batch verification: Multiple ops in one proof
- • Selective opening: Without revealing full model
- • Efficient proofs: Logarithmic proof size
- • Hierarchical: Natural fit for NN layers
Verification Process
Model Registration
Prover uploads weights with Tensor Commit. Commitment stored on-chain as canonical fingerprint.
Inference Execution
Prover runs forward pass, emits proof with opening, input embeddings, layer outputs, and Merkle path.
Verification
Every verifier checks every inference. ~2ms check time, gossip once, 2/3 BFT agreement needed.
Performance Comparison
| Operation | Latency | Proof Size | Gas Cost |
|---|---|---|---|
| TMATMUL 512x512 | 4.1 ms | 230 KB | 18K |
| TSTREAM 4x512 | 8.6 ms | 400 KB | 27K |
| TCOMMIT 70B | 22 ms | 470 KB | 120K |
* Gas costs based on base-load multiplier m = 1.0
LLM-Specific Optimizations
Token Embeddings
Committed polynomially with positional encoding using homomorphic properties
Layer Normalization
Mean/variance via polynomial commitments, inverse sqrt via polynomial approximation
Multi-Head Attention
Q, K, V matrices committed individually, attention scores polynomially approximated
Residual Connections
Handled via commitment homomorphism, layers reuse prior commitments
Mixture-of-Experts
Sparse expert activations committed efficiently, only activated experts contribute